poltlo.blogg.se

Information described below to the designated agent listed below. Or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one

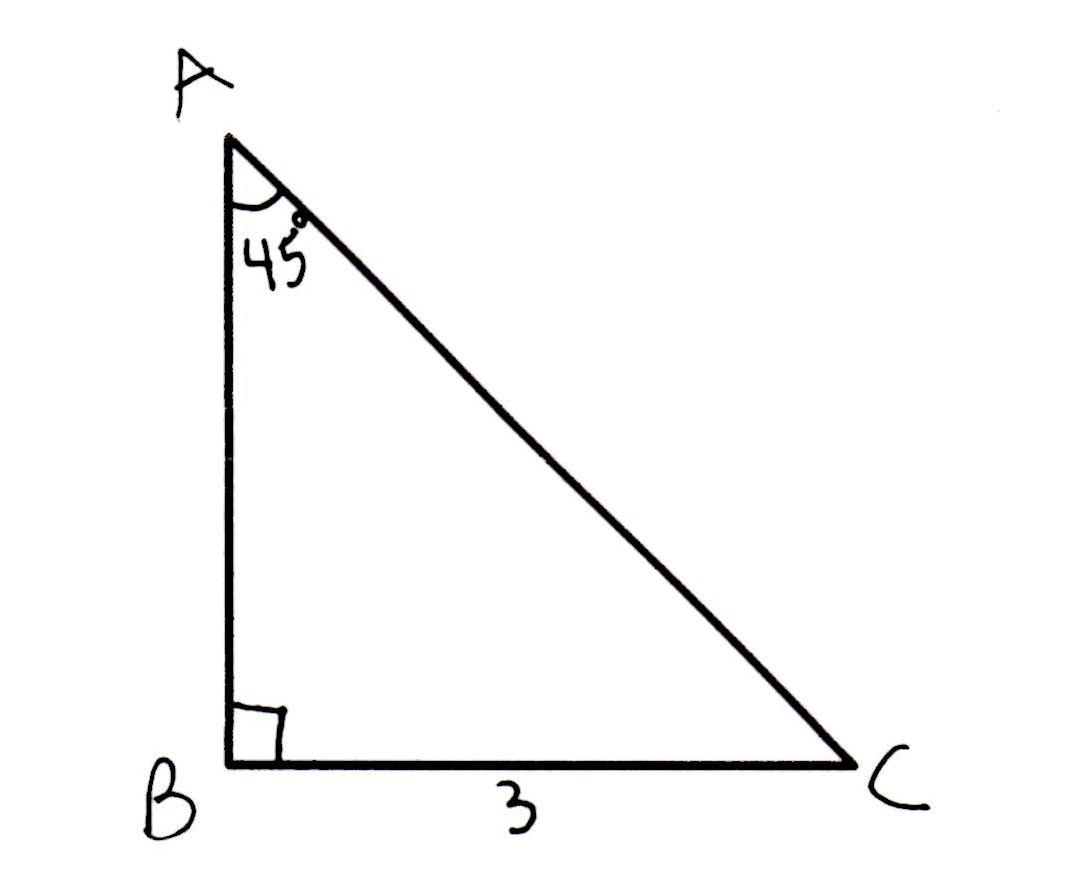
Therefore, using the triangle ratios, we have for the hypotenuse of our triangle, which is also the diagonal of our square. In this case, because it is the side length of our square and the triangles formed by the square's diagonal. Triangles have side length ratios of, where represents the side lengths of the triangle's legs and represents the length of the hypotenuse. Although one could solve this rather easily with Pythagorean Theorem, the following method could be faster. The second approach relies on recognizing a triangle. We can substitute these values into the equation and then solve for, the hypotenuse of the triangle and the diagonal of the square: Remember the formula:, where and are the lengths of the legs of the triangle, and is the length of the triangle's hypotenuse.

Once you recognize the right triangle in this question, you can begin to use the Pythagorean Theorem. Furthermore, the diagonal bisects two ninety-degree angles, thereby making the resulting triangles a triangle.įrom here you can go one of two ways: using the Pythagorean Theorem to find the diagonal, or recognizing the triangle as a triangle. By drawing the square out and adding the diagonal, you can see that you form two right triangles. The first step is to realize that this is really a triangle question, even though it starts with a square. The answer can be found two different ways.